Question

How do we do this one its one quiestion two parts

Answer 1

5.26 in × 14.48 in × 38.48 in

2930.82 in³

Step-by-step explanation:

You want the dimensions and volume of the maximum-volume open-top box that can be made from 25 in by 49 in stock when congruent squares are cut from the corners.

Dimensions

If the side length of the square is x, then the dimensions of the base of the box are (25 -2x) and (49 -2x) inches.

Volume

The volume of the box is the product of the dimensions:

V(x) = x(25 -2x)(49 -2x) = 4x³ -148x² +1225x

Maximum volume

The maximum volume will be had when x is such that the derivative of volume with respect to x is zero. The maximum value of x cannot be as great as 25/2 = 12.5 because that value gives a zero-width box.

V'(x) = 12x² -296x +1225 = 0

Final dimensions

Using the quadratic formula, we find the relevant value of x to be ...

`x=(-b-√(b^2-4ac))/(2a)=(-(-296)-√((-296)^2-4(12)(1225)))/(2(12))\\\\=(296-√(28816))/(24)=\boxed{(74-√(1801))/(6)\approx 5.2603}`

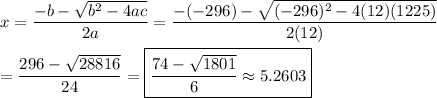
Then the dimensions are ...

x ≈ 5.2603

25 -2x ≈ 14.4794

49 -2x ≈ 38.4794

The box is about 5.26 inches by 14.48 inches by 38.48 inches.

Largest volume

The volume of the final box is about ...

(5.2603 in)(14.4794 in)(38.4794 in) ≈ 2930.82 in³

The volume of the finished box is about 2930.82 cubic inches.

__

Additional comment

As the attachment shows, a graphing calculator can show the extreme value(s) of the volume function, and the corresponding box dimensions.

Answer 2

Volume = 5861.64 cubic inches

Step-by-step explanation:

We were given that we should make an open rectangular box from a cardboard of dimension 25 inches by 49 inches

We are to cut congruent squares from the corners and folding up the sides

The box is open at the top

We will proceed to solve as shown below:

`\begin{gathered} Length=49in \\ Width=25in \\ \text{Taking a unit of square from each side, we have:} \\ New\text{ }Length=49-2x;x<24.5 \\ New\text{ }Width=25-2x;x<12.5 \\ Height=x \\ \text{So, the doamin of this is \lparen0, 12.5\rparen} \\ V(x)=x(49-x)(25-x) \\ V(x)=x^3-74x^2+1225x \\ \text{Taking the derivative of both sides, we have:} \\ V^(\prime)(x)=3x^2-148x+1225 \\ Equate\text{ }V^(\prime)(x)\text{ to zero, we have:} \\ 3x^2-148x+1225=0 \\ \text{Solving using quadratic formula, we have:} \\ x=38.81273011,10.52060321 \\ Either\text{ of these two values is either the maximum or minimum} \end{gathered}`

We will proceed as shown below:

Hence, the maximum volume is given by:

`\begin{gathered} x=10.52060321 \\ V(x)=x^3-74x^2+1225 \\ V(x)=5861.64in^3 \end{gathered}`