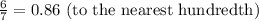Question

This probability distribution shows thetypical grade distribution for a Geometrycourse with 35 students.GradeAB.CDF3 2Frequency 51015Find the probability that a student earns agrade of A, B, or C.p = [?]Enter a decimal rounded to the nearest hundredth.

Answer 1

The probability of an event is obtained as follows:

`Pr(\text{Event)}=\frac{number\text{ of favourable outcomes}}{number\text{ of sample space}}`
`\begin{gathered} Pr(a\text{ student earns a grade of A) = }\frac{number\text{ of students that earn grade A}}{Total\text{ number of students}} \\ Pr(a\text{ student earns a grade of A)=}(5)/(35) \\ \\ Pr(a\text{ student earns a grade of B)=}\frac{number\text{ of students that earn grade B}}{Total\text{ number of students}} \\ Pr(a\text{ student earns a grade of B)=}(10)/(35) \\ \\ Pr(a\text{ student earns a grade of C)=}\frac{\text{number of students that earn grade C}}{Total\text{ number of students}} \\ Pr(a\text{ student earns a grade of C)=}(15)/(35) \end{gathered}`

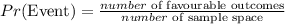
Therefore, the probability that a student earns a grade of A, B or C=

Pr(a student earns a grade of A) + Pr(a student earns a grade of B) + Pr(a student earns a grade of C).

This becomes;

`(5)/(35)+(10)/(35)+(15)/(35)=\text{ }(30)/(35)=(6)/(7)`

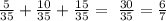
Hence, the probability that a student earns a grade of A, B or C is

`(6)/(7)=0.86\text{ (to the nearest hundredth)}`