Question

A sphere rotates about its axis, starting at 0 = Orad and finishing at 0 = 3.2 rad in 4.2 s. What is its average angular velocity?

Answer 1

Given:

The initial angular position, θ₁=0 rad

The final angular position, θ₂=3.2 rad

The time period, t=4.2 s

To find:

The angular velocity.

Step-by-step explanation:

The angular velocity is the time rate of change of angular displacement of the object.

Thus the angular velocity of the sphere is given by the ratio of the angular displacement to the time period.

Thus, the angular velocity of the sphere is given by,

`\omega=(\theta_2-\theta_2)/(t)`

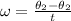
On substituting the known values,

`\begin{gathered} \omega=(3.2-0)/(4.2) \\ =0.76\text{ rad/s} \end{gathered}`

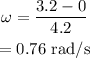
Final answer:

The angular velocity of the sphere is 0.76 rad/s