If the relationship between Angle 1 and Angle 2 is not given in the question, a figure must be provided for us to determine their relationships and make an equation out of it. Otherwise, this is an incomplete question.
For your guidance, let's make an example.
Let's apply all those given details from the question to this figure.
Angle 1 and Angle 2 are shown to be Supplementary Angles. This means that the total measures of the two angles when added up is equal to 180 degrees.
If Angle 1 and Angle 2 are shown to be Complementary Angles. This means that the total measures of the two angles when added up is equal to 90 degrees.
From this example relationship, the Angles are Supplementary, thus, we can finally make an equation:
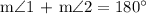
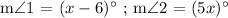
Let's substitute the given functions of Angle 1 and Angle 2 to the relationship equation to find the value of x. We get,
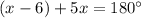
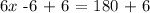
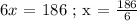
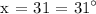
Since we now have the value of x which is 31 degrees. Let's now compute the measure of Angle 1 and Angle 2.
Angle 1 = (x -6) = 31 - 6 = 25 degrees
Angle 2 = (5x) = 5(31) = 155 degrees