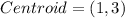Given the vertices of the triangle ABC:
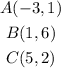
You can use the following formula to find the x-coordinate of the Centroid:
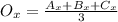
And this formula to find the y-coordinate of the Centroid:
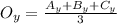
In this case, you know that:
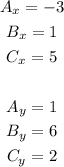
Therefore, substituting values into the formulas and evaluating, you get:
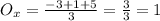
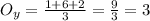
Hence, the answer is: