Question

Hello what are the answers to ABC D & E

Answer 1

We are given the graphs of two functions f(x) and g(x) and we are asked to determine the following operations:

`(f+g)(x)`

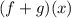
Part (a): To determine the sum of the two functions we need to have into account the sum of two functions is given by the following relationship:

`(f+g)(x)=f(x)+g(x)`

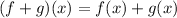
Since we are required to determine this value at x = -2 we replace "x" in the functions for -2:

`(f+g)(-2)=f(-2)+g(-2)`

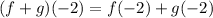
Therefore, we need to determine the values of f(-2) and g(-2), we do this using the corresponding graphs. From the graphs we obtained to values:

`\begin{gathered} f(-2)=4 \\ g(-2)=-2 \end{gathered}`

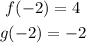
We obtained them like this:

Now we replace these values and we get:

`(f+g)(-2)=4-2=2`

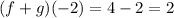
Therefore, the sum of the functions is 2.

Part (b). We are asked to determine the following:

`(f+g)(-1)`

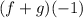
We use a relationship similar to the previous one:

`(f+g)(-1)=f(-1)-g(-1)`

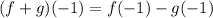
Now we determine the values of f(-1) and g(-1) from the graph and we get:

`\begin{gathered} f(-1)=1 \\ g(-1)=-3 \end{gathered}`

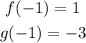
In the graph it looks like this:

Now we replace the values and we get:

`(f+g)(-1)=1-(-3)=1+3=4`

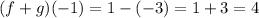
Therefore, the difference of the function at x = -1 is 4.

Part (b): We are asked to determine the production of the function at x = 0. We use the following relationship:

`(fg)(0)=f(0)g(0)`

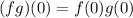
Now we determine the values of the function at x = 0:

`\begin{gathered} f(0)=0 \\ g(0)=-4 \end{gathered}`

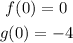
In the graph it looks like this:

Replacing the values we get:

`(fg)(0)=(0)(-4)=0`

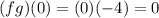
Part (d). we are asked to determine the composition of the two functions at x = 0. To do that we use the following relationship:

`(g\circ f)(0)=g(f(0))`

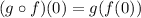
Therefore, we need first to determine the value of f(0) and then evaluate g(x) at that value. The value of f(0) we obtained it in point C and it is:

`f(0)=0`

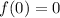
Replacing this value we get:

`(g\circ f)(0)=g(0)`

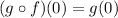
Now we use the value of g(0) that we got in point C:

`g(0)=-4`

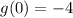
therefore, the composition is:

`(g\circ f)(0)=-4`

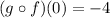
Part E: We are asked to determine the quotient between the two functions:

`((f)/(g))(-1)=(f(-1))/(g(-1))`

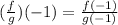
We use the values of the functions at x = -1 that we determined in part B. those values are:

`\begin{gathered} f(-1)=1 \\ g(-1)=-3 \end{gathered}`

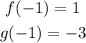
Replacing the values:

`((f)/(g))(-1)=(1)/(-3)=-(1)/(3)`

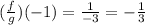
Therefore, the quotient of the functions is -1/3.