Question

Identify intervals on which the function is (a) increasing, (b) decreasing, and (c) constant. In each case, assume that the domain of the function is (-∞, ∞) and that any characteristics of the graph continue as indicated.

Answer 1

`\begin{gathered} (-\infty,1\rbrack,decreasing \\ (1,\infty)increasing \end{gathered}`

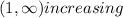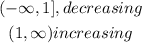
1) In this question, we need to remind ourselves of the definition of an increasing or decreasing interval.

2) When the function is increasing we have:

`x_2>x_1,f(x_2)>f(x_1)`

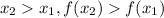
On the other hand, a given interval of a function is decreasing when:

`x_2>x_1,f(x_2)<strong>3) </strong>Examining the graph we see two intervals:[tex]\begin{gathered} (-\infty,1\rbrack \\ (1,\infty) \end{gathered}`

Note that for the first interval the more the f(x) values increase the x values decrease.

So,

`\begin{gathered} (-\infty,1\rbrack,decreasing \\ \end{gathered}`

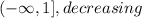
And on the other hand, the more the x values increase the more the f(x) values increase, so:

`(1,\infty)increasing`