Question

Solve question b only please, thanks

Answer 1

a) 54,975.58 km (2 d.p.)

b) 43

Explanation:

Part (a)

We start with 1 sheet of paper.

Step 1: After tearing it in half, we have 2 pieces of paper.

Step 2: After tearing them in half, we have 4 pieces of paper.

Step 3: After tearing them in half, we have 8 pieces of paper.

Therefore, we can see that each time we tear the pieces of paper in half, we double the number of pieces we have.

We can model this as a geometric sequence, where the initial term "a" is 2 (the number of pieces after the first tear) and the common ratio "r" is 2.

Therefore, the equation for the nth term is:

`\implies a_n=2 (2)^(n-1)`

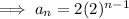
If we repeat the process 40 times, the total number of pieces of paper can be calculated by substituting n = 40 into the equation for the nth term:

`\implies a_(40)=2(2)^(40-1)`

`\implies a_(40)=2(2)^(39)`

`\implies a_(40)=2^1 \cdot 2^(39)`

`\implies a_(40)=2^(1+39)`

`\implies a_(40)=2^(40)`

`\implies a_(40)=1\;099\;511\;627\;776`

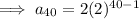
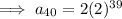
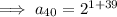
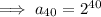
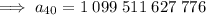
Therefore, after repeating the tearing process for a total of 40 times, we will have 1,099,511,627,776 pieces of paper.

Given each piece of paper is approximately 0.05 mm thick, to calculate how high the stack of paper will be (in mm) if the pieces are placed one on top of each other, multiply the total number of pieces of paper by 0.05 mm:

`\implies 1\;099\;511\;627\;776* 0.05=54\;975\;581\;388.8\; \sf mm`

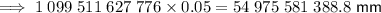
As there are 1,000,000 millimeters in a kilometer, divide the height in millimeters by 1,000,000 to find the height in kilometers:

`\implies (54\;975\;581\;388.8)/(1\;000\;000)=54\;975.58\; \sf km\;(2\;d.p.)`

Therefore, the stack of paper would be approximately 54,975.58 km (2 d.p.) high if the pieces are placed one on top of the other.

Part (b)

Calculate the height of each piece of paper in terms of kilometers by dividing the height in millimeters by 1,000,000:

`\implies (0.05)/(1\;000\;000)=0.000\;000\;05\; \sf km`

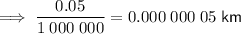
To find the height of the stack of paper in kilometers given the process of tearing is repeated for a total of n times, multiply the equation we found in part (a) by the height of a piece of paper in kilometers.

Therefore, the height "h" of a stack of pieces of paper (in km) where the process of tearing is repeated for a total of n times is:

`\implies h=2 (2)^(n-1) * 0.000\;000\;05`

`\implies h=0.000\;000\;1 (2)^(n-1)`

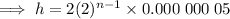
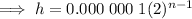
To calculate how many times the process would have to be repeated for the stack to reach 384,400 km in height, substitute h = 384,400 into the equation and solve for n:

`\implies 384\;400=0.000\;000\;1 (2)^(n-1)`

`\implies (384\;400)/(0.000\;000\;1)= (2)^(n-1)`

`\implies 3\;844\;000\;000\;000= (2)^(n-1)`

`\implies \ln (3\;844\;000\;000\;000)= \ln (2)^(n-1)`

`\implies \ln (3\;844\;000\;000\;000)= (n-1)\ln (2)`

`\implies (\ln (3\;844\;000\;000\;000))/(\ln (2))= n-1`

`\implies (\ln (3\;844\;000\;000\;000))/(\ln (2))+1=n`

`\implies n=42.805\;745\;47...`

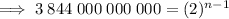
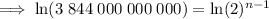
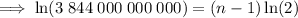
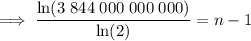
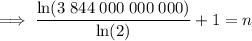
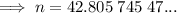
Therefore, the process would have to be repeated 43 times for the stack to first reach the moon, 384,400 km away.