Answer:
34.9° by the Law of Cosines
Explanation:
To solve this, we first have to know when to use the Law of Sines and when to use the Law of Cosines.
When to use the Law of Sines:
Use the Law of Sines when you have two angles and a side, or two sides and an angle, and you want to find the missing angle or side.
The Law of Sine states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is the same for all three sides of the triangle:
 .
.
When to use the Law of Cosines:
Use the Law of Cosines when you have two sides and the included angle, or all three sides of a triangle, and you want to find the missing angle or side.
The Law of Cosines states:
 ,
,
where A is the angle included between sides b and c.
For the triangle given in the question, we have all three sides and need to find a missing angle. Therefore the Law of Cosines must be used:
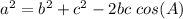
⇒ 18² = 30² +30² - 2(30)(30) × cos(
 )
)
⇒ 324 = 1800 - 1800·cos(
 )
)
⇒ 1800·cos(
 ) = 1800 - 324
) = 1800 - 324
⇒ 1800·cos(
 ) = 1476
) = 1476
⇒ cos(
 ) =
) =
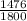
⇒ cos(
 ) = 0.82
) = 0.82
⇒
 = cos⁻¹(0.82)
= cos⁻¹(0.82)
⇒
 = 34.9°
= 34.9°