We have to calculate in how many ways can the letters in the word PARALLEL be arranged.
We start by listing the unique letters and how many times each one appear in the word.
We have one P, two A's, one R, three L's and one E, for a total of 8 letters.
We then can express this as a permutation like this:
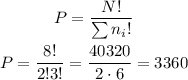
NOTE: "ni" is the number of repetitions of each letter that repeats more than one time. In this case, we have two A's and three L's.
Answer: there are 3360 permutations.