Question

If you need $20,000 six years from now, what is the minimum amount of money you need to deposit into a bank account that pays 3% annual interest, compounded (give your answers to the nearest cent):a) annually? $______b) monthly? $_____c) daily (assuming 365 days in a year)? $ _____

Answer 1

To solve the question, we would be making use of the compound interest formula. This is given as;

`A=P(1+(r)/(n))^(nt)`

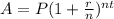
A=final amount = $20,000

P=initial principal balance

r=interest rate =3%

n=number of times interest applied per time period

t=number of time periods elapsed = 6 years

Part A

If the interest is compounded annually, n =1

Therefore;

`\begin{gathered} 20000=P(1+(0.03)/(1))^(1*6) \\ 20000=P(1+0.03)^6 \\ (1.03)^6P=20000 \\ P=(20000)/((1.03)^6) \\ P=16749.69 \end{gathered}`

Answer: The minimum amount would be $16749.69

Part B

If the interest is compounded monthly, n =12

`\begin{gathered} 20000=P(1+(0.03)/(12))^(6*12) \\ 20000=P((12+0.03)/(12))^(72) \\ ((12.03)/(12))^(72)P=20000 \\ P=(20000)/(((12.03)/(12))^(72)) \\ P=16709.16 \end{gathered}`

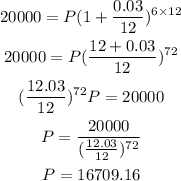
Answer: The minimum amount would be $16709.16

Part C

If the interest is compounded monthly, n =365

`\begin{gathered} 20000=P(1+(0.03)/(365))^(365*6) \\ 20000=P((365+0.03)/(365))^(2190) \\ ((365.03)/(365))^(2190)P=20000 \\ P=(20000)/(((365.03)/(365))^(2190)) \\ P=16705.53 \end{gathered}`

Answer: The minimum amount would be $16705.53