Question

Flashlight problem: you shine a flashlight, making a circular spot of light on the wall with radius 5cm. As you back away from the wall, the radius increases at the rate of 7 cm/s. Let t be the number of seconds since you started backing away. Let r(t) be the radius of the spot of light, in centimeters. Let a(r(t)) be the area of the spot, in square centimeters. Write an equation for r(t) as a function of t. Write another equation for a(r(t)) as a function of r(t). Write a third equation for alr() explicitly in terms of t. Show that the last equation gives the correct area for timest = 4s and t = 7 s.

Answer 1

If we let t be the number of seconds since you started backing away and we let r(t) be the radius of the spot of light in centimeters.

r(t) =5 + 7t

If we let a(r(t)) to be the area of the spot,

`A=\pi r^2`

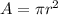
where A = a(r(t)) and r= 5 + 7t

a(r(t)) = π (5+7t)²

a(r(t)) = π (49t² + 70t +25)

For t=4s

a(r(4)) = π[49(4)²+70(4)+25]

=1089π cm²

For t=7s

a(r(7)) = π[49(7)²+70(7)+25]

=2916 π cm²