Question

(05.06)

Choose the graph below that represents the following system of inequalities: (1 point)

y ≥ −3x + 1

y ≥ 1 over 2 x + 3

Graph of two lines that intersect at one point. Both lines are solid. One line passes through points negative 2, 2 and 0, 3 and is shaded above the line. The other line passes through points 0, 1 and 1, negative 2 and is shaded above the line.
Graph of two lines that intersect at one point. Both lines are solid. One line passes through points negative 2, 2 and 0, 3 and is shaded below the line. The other line passes through points 0, 1 and 1, negative 2 and is shaded above the line.
Graph of two lines that intersect at one point. Both lines are solid. One line passes through points negative 2, 2 and 0, 3 and is shaded below the line. The other line passes through points 0, 1 and 1, negative 2 and is shaded below the line.
Graph of two lines that intersect at one point. Both lines are solid. One line passes through points negative 2, 2 and 0, 3 and is shaded above the line. The other line passes through points 0, 1 and 1, negative 2 and is shaded below the line.

Answer 1

The shading above the first line and below the second line indicates the regions that satisfy both inequalities simultaneously.

Explanation:

The correct graph that represents the given system of inequalities is:

Graph of two lines that intersect at one point. Both lines are solid. One line passes through points negative 2, 2 and 0, 3 and is shaded above the line. The other line passes through points 0, 1 and 1, negative 2 and is shaded below the line.

This graph satisfies both inequalities: y ≥ -3x + 1 and y ≥ 1/2x + 3. The shading above the first line and below the second line indicates the regions that satisfy both inequalities simultaneously.

Answer 2

A) Graph of two lines that intersect at one point. Both lines are solid. One line passes through points (-2, 2) and (0, 3) and is shaded above the line. The other line passes through points (0, 1) and (1, -2) and is shaded above the line.

Explanation:

Given system of inequalities:

`\begin{cases} y \geq -3x+1\\\\y \geq (1)/(2)x+3\end{cases}`

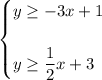
When graphing inequalities:

• < or > : dashed line
• ≤ or ≥ : solid line
• < or ≤ : shading under the line
• > or ≥ : shading above the line

To graph linear inequalities, treat them as equations (swap the inequality sign for an equals sign). Plug in two values of x to find two points on the line to help draw the lines.

Graphing the line y ≥ -3x + 1

Substitute x = 0 and x = 1 into the equation of the inequality to find two points on the line.

`\begin{aligned}x=0 \implies y&=-3(0)+1\\y&=1\end{aligned}`

`\begin{aligned}x=1 \implies y&=-3(1)+1\\y&=-3+1\\y&=-2\end{aligned}`

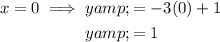
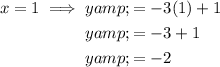
Plots points (0, 1) and (1, -2).

As the inequality sign is ≥, draw a solid line through the plotted points and shade above the line.

Graphing the line y ≥ (1/2)x + 3

Substitute x = -2 and x = 0 into the equation of the inequality to find two points on the line.

`\begin{aligned}x=-2 \implies y&=(1)/(2)(-2)+3\\y&=-1+3\\y&=2\end{aligned}`

`\begin{aligned}x=0 \implies y&=(1)/(2)(0)+3\\y&=0+3\\y&=3\end{aligned}`

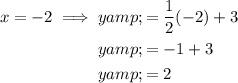
Plots points (-2, 2) and (0, 3).

As the inequality sign is ≥, draw a solid line through the plotted points and shade above the line.

Solution

The description of the graph that represents the given system of inequalities is:

• Graph of two lines that intersect at one point. Both lines are solid. One line passes through points (-2, 2) and (0, 3) and is shaded above the line. The other line passes through points (0, 1) and (1, -2) and is shaded above the line.