Answer:
- m∠A = 24°
- m∠B = 132°
- m∠C = 24
Explanation:
ΔABC is an isosceles triangle, which is indicated by the marks on the two sides.
Isosceles triangles are triangles that have two equal side lengths and angles. So here, ∠A and ∠C have the same angle measures.
Additionally, the sum of the three angles of any triangle sums up to 180°.
..................................................................................................................................................
Given: m∠A = 8x, m∠B = 44x, and m∠C = 8x
Step 1: Set the measure of the angles to equal 180.


Step 2: Divide both sides by 60.

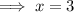
Step 3: To find the measure of each angle, substitute 3 for x.



The measures of ∠A, ∠B, and ∠C all sum up to 180°.