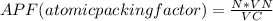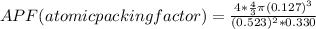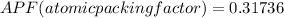Question

Consider a hypothetical metal that has a density of 11.6 g/cm3, an atomic weight of 157.6 g/mol, and an atomic radius of 0.127 nm. Compute the atomic packing factor if the unit cell has tetragonal symmetry; values for the and lattice parameters are 0.523 nm and 0.330 nm, respectively.

Answer 1

`APF(atomic packing factor)=0.31736`

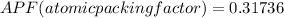
Step-by-step explanation:

From the question we are told that

Density of metal
`\rho=11.6 g/cm3`

Atomic weight of
`W=157.6 g/mol`

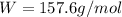
Atomic radius of
`r= 0.127 nm`

Lattice parameters=>
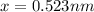`x=0.523nm` and
`y=0.330 nm`

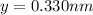
Generally the equation for atomic packing factor is mathematically given as

`APF(atomic packing factor)=(Spere's\ volume)/(unit\ cell\ volume)`

`APF(atomic packing factor)=(N*VN)/(VC)`

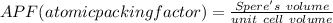
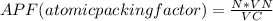
Generally the equation for number of atoms N is mathematically given as

`N=(\rho )/(atomic raduis*Avacados constant)`

`N=(11.6 )/(0.127*10^(-9)*6.02214086*10^(23) mol-1)`

`N=4`

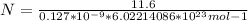
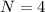
Therefore APF(atomic packing factor)

`APF(atomic packing factor)=(N*VN)/(VC)`

`APF(atomic packing factor)=(4*(4)/(3) \pi (0.127)^3)/((0.523)^2 *0.330)`

`APF(atomic packing factor)=0.31736`