Question

The

expression 10x²2 - 19x +
6 can be written as (2x - 3)(5x
+ d) where d represents a
number. What is the value of
d?
5 points
E
u:
Tr
ex
al

Answer 1

d = -2

Explanation:

This is a quadratic expression, where
`ax^2 + bx + c=(2x-3)(4x+d)`

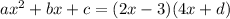
To get it in the form with the brackets, we must factorise the expression.

The most common method to do this is known as 'splitting the middle.

Starting with our expression, 10x² - 19x + 6, we need to split the middle term into two terms so we can have 4 terms, and thus we can factorise each pair of terms. To do this, we multiply the leading coefficient (10), with the constant term (6).

Now using the result and the coefficient of the middle term (19), we need to find two integers that multiply to give 60 (6×10), AND also add to give 19.

Also taking into account the sign of the middle term, if the middle term is negative, but the constant term is positive then the two numbers you are trying to find will each be negative. If both the middle term and constant term are negative, then the numbers you are trying to find will be negative and positive. If both the middle and constant terms are positive, then both numbers are positive.

Therefore, the numbers we are looking for are: -15 and -4. -15×-4=60. -15-4=19. Now we split the middle term into two terms, where these two numbers are the coefficients of x.

`10x^2-15x-4x+6`

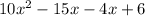
Now, we factorise each pair of terms.

`5x(2x-3)-2(2x-3)`

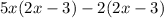
As you can see, we now have two terms, and both have (2x-3). Therefore, we can factorise this term out:

`(2x-3)(5x-2)`

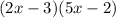
Therefore, d = -2