Question

Perpendicular to the line y=3x +8; passes through (-4,1)

Answer 1

Comparing y=3x+8 with straight line equation y=mx+c, where m is the slope, we get

Slope of line y=3x+8, m=3.

The slope of a line perpendicular to y=3x+8 is,

`\begin{gathered} m_1=(-1)/(m) \\ =(-1)/(3) \end{gathered}`

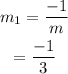
The coordinates of a point passing through perpendicular line to y=3x+8 is (x0,y0)=(-4,1).

Now, use point slope formula to find the equation of a line passing through (x0,y0)=(-4,1) with slope m1.

`\begin{gathered} m_1=(y-y_0)/(x-x_0) \\ (-1)/(3)=(y-1)/(x-(-4)) \\ (-1)/(3)=(y-1)/(x+4) \\ -x-4=3y-3 \\ -x-1=3y \\ \end{gathered}`

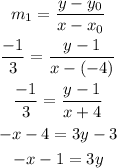
Therefore, the equation of a line perpendicular to the line y=3x +8 and passes through (-4,1) is -x-1=3y.