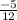Question

Evaluate tan( sin^-1 ( -5/13))​

Answer 1

`-(5)/(12)`

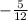
Explanation:

Ф = angle of interest

=
`sin^(-1) ((-5)/(13))`

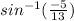
Taking sin on both sides of the equation to get rid of the
`sin^(-1)`:

sinФ =
`sin[sin^(-1) ((-5)/(13))]`

∴sinФ =
`(-5)/(13)`

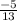
Recalling the formula for the trigonometric function sinФ:

sinФ =
`(Opposite)/(Hypotenuse)`

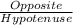
Deducing the measurements of the right- angled triangle with respect to the Ф angle:
opp = Opposite = -5 units

hyp = Hypotenuse = 13 units

∴adj = Adjacent can be determined using the Pythagorean Theorem:

`hyp^(2) = opp^(2) + adj^(2)`

`13^(2) = (-5)^(2) + adj^(2)`

`adj^(2) = 13^(2) - 5^(2)`

`= 169 - 25`

`= 144`

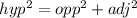
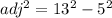
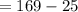
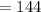
Taking square root on both sides to get rid of the square:

`\sqrt{adj^(2)} = √(144)`

∴ adjacent = 12 units

Now apply the trigonometric function tanФ

tanФ =
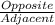
`(Opposite)/(Adjacent)`

=
`(-5)/(12)`