Question

Verify the trig identity 1/tan + tan= sec^2/ tan
`\tan( \sec - (\pi)/(4) ) = ( \tan( \sec( - 1) ) )/(1 + \tan( \sec(?) ) )`

Answer 1

Starting with the equation:

`(1)/(\tan(x))+\tan (x)=(\sec ^2(x))/(\tan (x))`

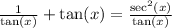
Take the expression on the right hand side of the equation:

`(\sec ^2(x))/(\tan (x))`

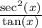
From the Pythagorean Identity and the definition of secant, we can prove that:

`1+\tan ^2(x)=\sec ^2(x)`

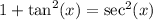
That fact can be verified as follows: the Pythagorean Identity states that:

`\sin ^2(x)+\cos ^2(x)=1`

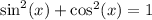
Divide both sides by the squared sine of x: