Question

Please show your work.

Answer 1

1) You should add 49 to both sides to complete the square.

`\textsf{Solutions:}\;\;\;x=3,\;\;x=-17`

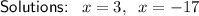
2) The discriminant of the equation is 261.

There are 2 solutions.

`\textsf{Solutions:}\;\;\;n=(1 +3√(29))/(10),\;\;n=(1 -3√(29))/(10)`

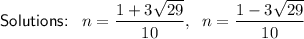
Explanation:

Question 1

Given quadratic equation:

`x^2+14x-51=0`

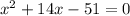
To solve the given quadratic equation by completing the square, first move the constant to the right side of the equation:

`\implies x^2+14x=51`

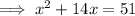
Add the square of half the coefficient of the term in x to both sides:

`\implies x^2+14x+\left((14)/(2)\right)^2=51+\left((14)/(2)\right)^2`

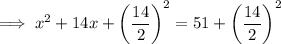
Simplify:

`\implies x^2+14x+\left(7\right)^2=51+\left(7\right)^2`

`\implies x^2+14x+49=51+49`

`\implies x^2+14x+49=100`

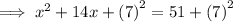
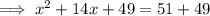
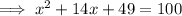
Therefore, we added 49 to both sides of the equation to complete the square.

To solve, factor the perfect square trinomial on the left side of the equation:

`\implies (x+7)^2=100`

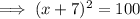
Square root both sides:

`\implies √((x+7)^2)=√(100)`

`\implies x+7=\pm10`

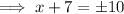
Subtract 7 from both sides of the equation:

`\implies x=-7\pm10`

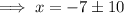
Therefore, the solutions are:

`x=3,\;\;x=-17`

Question 2

`\boxed{\begin{minipage}{4 cm}\underline{Quadratic Formula}\\\\$x=(-b \pm √(b^2-4ac))/(2a)$\\\\when $ax^2+bx+c=0$ \\\end{minipage}}`

Given quadratic equation:

`5n^2-n=13`

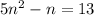
To solve using the quadratic formula, subtract 13 from both sides so that the equation is in the form ax² + bx + c = 0:

`\implies 5n^2-n-13=0`

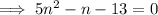
Therefore:

• a = 5
• b = -1
• c = -13

The discriminant of the equation is b² - 4ac:

`\begin{aligned}\implies b^2-4ac&=(-1)^2-4(5)(-13)\\&=1+260\\&=261\end{aligned}`

Therefore, the discriminant is 261.

As the discriminant is positive, there are 2 solutions.

To find the solutions, substitute the values of a, b and c into the quadratic formula and solve for n:

`\implies n=(-(-1) \pm √((-1)^2-4(5)(-13)))/(2(5))`

`\implies n=(1 \pm √(1+260))/(10)`

`\implies n=(1 \pm √(261))/(10)`

`\implies n=(1 \pm √(9\cdot29))/(10)`

`\implies n=(1 \pm3√(29))/(10)`

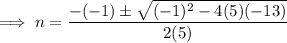
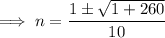
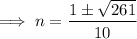
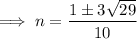
Therefore, the solutions are:

`n=(1 +3√(29))/(10),\;\;n=(1 -3√(29))/(10)`