Question

One closed organ pipe has a length of 1.44 meters. When a second pipe is played at the same time, a beat note with a frequency of 1.3 hertz is heard. By how much is the second pipe too long?

Answer 1

Given:

Length of pipe = 1.44 m

Frequency of second pipe = 1.3 Hz

Let's find the difference between the lengths of the pipes.

Here, we have:

`f_(beat)=f_1-f_2`

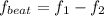
Thus, we have:

`f_2=f-1.3`

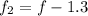
To find the frequency of the pipe, f,, we have:

`\begin{gathered} f=(v)/(4l) \\ \\ Where: \\ v\text{ is the speed of sound = 343 m/s} \\ \\ f=(343)/(4*1.44) \\ \\ f=59.55\text{ Hz} \end{gathered}`

Plug in the value of f and find f2:

`\begin{gathered} f_2=59.55-1.3 \\ \\ f_2=58.25\text{ Hz} \end{gathered}`

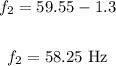
Now, let's find the length of the second pipe:

`\begin{gathered} f=(v)/(4l) \\ \\ l_2=(v)/(4f_2) \\ \\ l_2=(343)/(4*58.25) \\ \\ l_2=1.47\text{ m} \end{gathered}`

Therefore, the difference in length will be:

L2 - L1 = 1.47 m - 1.44 m = 0.03 m

Therefore, the second pipe will be longer by 0.03 meters.

ANSWER:

0.03 m