Question

Find PQ.
Write your answer as an integer or as a decimal rounded to the nearest tenth.

Answer 1

PQ = 3.4

Explanation:

Pre-Solving

We are given the right triangle (notice the right angle) PQR. We know that the length of QR is 6, and that m<PQR is 56°.

We want to find the length of PQ.

Solving

We can use trigonometry to solve this. Recall the following identities:

Sine is
`(opposite)/(hypotenuse)`

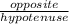
Cosine is
`(adjacent)/(hypotenuse)`

Tangent is
`(opposite)/(adjacent)`

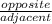
The "opposite" and "adjacent" sides are used in reference to a specific angle.

The angle that we will use as reference will be <PQR.

The opposite side will be the side that is opposite of the angle - in this case, it will be PR.

The adjacent side will be the side that is adjacent to the opposite side; in this case, it will be PQ.

The hypotenuse is always the side that is opposite to the right angle, so the hypotenuse will be QR.

Since we know the value of the hypotenuse, and we want to find the adjacent side, we should use the cosine of <PQR, or cos56 (as we are referencing everything using <PQR).

So, as an equation, this will be:

`cos( < PQR) = (PQ)/(QR)`

We can substitute our values in to get:

`cos56 = (PQ)/(6)`

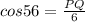
We can multiply both sides by 6 to get:

6(cos56) = PQ

Plug 6(cos56) into your calculator. Make sure that it is in degree mode.

3.355 ≈ PQ

We should round this to the nearest tenth, so PQ = 3.4.