Problem
A stack of 200 billion pennies would reach from Earth to the moon." 1. Use unit analysis to determine the number of pennies that are required to reach from Earth to the moon. The average distance between Earth and the moon is 238,857 miles. There are about 18 pennies in a 1-inch stack of pennies. Show all work (this includes the appropriate use of unit analysis). (2) I fact Rin yrd=3fr 17 pls help im rlly bad at unit analysis
Solution
We know that the distance between Earth and the Moon is d=238857 miles
We also know that 18 pennis are approximately in a 1 inch stack, so we can write this rate:
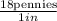
from units conversion we know that 1 mi = 63360 inches
So we can do the following:
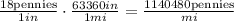
and we can find the number of pennis on this case with this operation
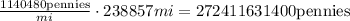
that correspond to approximately 272411 millions