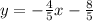Question

Find the equation of the line passing through the line (3,- 4) and (8, - 8)

Answer 1

`y=-(4)/(5)x-(8)/(5)`

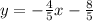
First, let us find the slope of the line using the following equation:

`m=(y_2-y_1)/(x_2-x_1)`

Using the points (3, -4) and (8, -8)

`m=(y_2-y_1)/(x_2-x_1)\Rightarrow m=(-8-(-4))/(8-3)`
`m=(-8+4)/(8-3)=(-4)/(5)\Rightarrow m=-(4)/(5)`

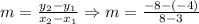
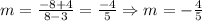
Now that we found the slope of the line, we are going to use the following equation to solve for the equation of the line:

`y-y_1=m(x-x_1)`

Using the point (3, -4)

`y-y_1=m(x-x_1)\Rightarrow y-(-4)=-(4)/(5)(x-3)`
`y+4=-(4)/(5)x+(12)/(5)\Rightarrow y=-(4)/(5)x+(12)/(5)-4`
`y=-(4)/(5)x-(8)/(5)`

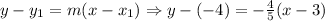
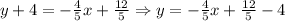
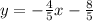
Therefore, the equation of the line that passes through the points (3, -4) and (8, -8) is:

`y=-(4)/(5)x-(8)/(5)`