Question

need help finding: a. Find the length of AB.b. Find the area of the sector AOBC. Find the length of ACd. Find the area of the sector AOC

Answer 1

The axis are perpendicular, therefore, the angles between the axis are equal to 90º.

`m∠BOC=90^o`

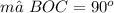
The angle ∠BOC is given by the sum of the angles ∠AOC and ∠AOB.

`m∠AOC+m∠AOB=m∠BOC`

The segment AO is the hypotenuse of a right triangle, and the coordinates of the point A represent the side length of the legs. With this information, we can find the measure of the angles ∠AOC and ∠AOB.

Given an angle on a right triangle, the ratio between the opposite side to this angle and the adjacent side is equal to the tangent of the angle. Using this information and the scheme above, we have the following relation

`\begin{gathered} \tan(AOC)=((-7))/((1)) \\ m\angle AOC=\arctg(-7) \\ m\angle AOC=81.8698976458... \end{gathered}`

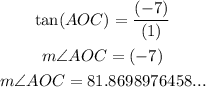
Since this angle is complementar to ∠AOB, we have

`\begin{gathered} 90^o-m\angle AOC=m∠AOB \\ \implies m∠AOB=8.13010235416... \end{gathered}`

And finally, to calculate all the items we also need the radius. Since this circle is centered at the origin, we can use the formula distance at the point A to find the radius.

`r=√(1^2+(-7)^2)=√(50)`

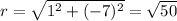
The arc associated to an angle is given by the formula

`arc=\theta*((\pi)/(180))* r`

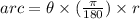
Where θ represents the angle in degrees.

Using this formula for item a), we have

`\begin{gathered} AB=8.13010235416...*((\pi)/(180))*√(50) \\ =1.00336369541... \\ \approx1.0 \end{gathered}`

The length of AB is equal to 1.0 units.

item b)

The area of a circle is given by the formula

`A=\pi r^2`

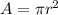
In our problem, we have sections of the circle. We can find the proportion by dividing the angle of the section by 360º, and then multiplying the result by the total area of the circle

`\begin{gathered} A=\pi*(√(50))^2*((8.13010235416...)/(360))=3.54742636511... \\ A\approx3.5 \end{gathered}`

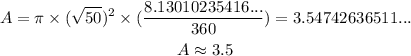
The area of the sector AOB is 3.5 square units.

item c)

Using the same formula we used for item a), we have

`\begin{gathered} AC=81.8698976458...*((\pi)/(180))*√(50) \\ =10.10384365... \\ \approx10.1 \end{gathered}`

The length of AC is 10.1 units.

item d)

The area for this section is given by the same expression used on item b).

`\begin{gathered} A=\pi*50*((81.8698976458...)/(360))=35.7224818047... \\ A\approx35.7 \end{gathered}`

The area of the sector AOC is 35.7 square units.