The system described in the question can be presented diagrammatically as shown below:
We can then bring out a diagram to solve as follows:
The angle θ is the required angle that we are to solve for.
We can use the Tangent Trigonometric Ratio to solve. The ratio is given to be

From the triangle,
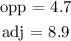
Substituting these values, we have
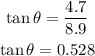
We can then find the angle to be
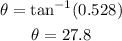
The angle between the ladder and the wall is 27.8°.