Question

Hi dear how do you have to do the math question e and f) It was when the rocket is moving 35ft/s how fast it’s velocity change in

Answer 1

Question

Step-by-step explanation

we are given the height function as:

`h(t)=16.1t^2-1.75t^3\text{ }`

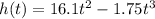
The first step will be to get the velocity function

`h^(\prime)(t)=32.2t-5.25t^2`

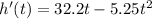
The acceleration is given by

`acceleration=h^(\prime)^(\prime)(t)=32.2-10.5t`

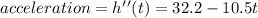
Since we are told to find how high the rocket will be at an instant of 10ft/s²

Therefore, we will equate the acceleration formula to 10ft/s² so that we will obtain t

`\begin{gathered} 10=32.2-10.5t \\ 10.5t=32.2-10 \\ 10.5t=22.2 \\ t=2.11428 \end{gathered}`

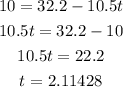
The final step will be to substitute t =2.11428 into the initial height function

`\begin{gathered} h=16.1\cdot\:2.11428^2-1.75\cdot\:2.11428^3=55.43027 \\ h=55.43\text{ ft} \\ \end{gathered}`

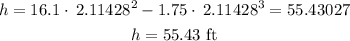
The answer is h = 55.43 ft

Part F

was when the rocket is moving 35ft/s, we will have to equate 35ft/s into the velocity formula

`\begin{gathered} h^(\prime)(t)=32.2t-5.25t^2=35 \\ \\ t_(1,\:2)=(-3220\pm \:140√(154))/(2\left(-525\right)) \\ \\ t=1.4120\:t=4.7212 \\ \\ \end{gathered}`

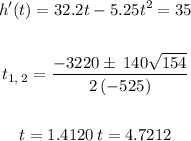
But we are told that t cannot be greater than 4

So that t=4.7212s is invalid

Thus, our value for t= 1.4120

So we will substitute this to get the acceleration

`\begin{gathered} =32.2-10.5(1.4120) \\ =17.374ft\text{/s}^2 \end{gathered}`

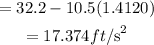
The answer is 17.37 ft/s²