Question

I need help with “solving a word problem using a quadratic equation with irrational roots”. Thank you so much I will include a picture

Answer 1

The values of t are 1.42 or 0.70

Step-by-step explanation:
`\begin{gathered} \text{Given:} \\ h\text{ = }4+34t-16t^2 \end{gathered}`

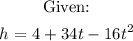
To find the values of t for which height is 20 feet,, we will substitute 20 for h in the equation above:

`20=4+34t-16t^2`

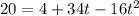
Next we will solve for t:

`\begin{gathered} \text{subtract 20 from both sides:} \\ 20-20=4+34t-16t^2\text{ - 20} \\ 0=34t-16t^2\text{ - 16} \\ \\ re\text{ writing:} \\ 16t^2\text{ -34t + 16 = 0} \end{gathered}`

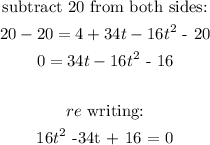
Since we can't easily ascertain if it is factorisable using factorisation method, we will use the formula method to factorise it:

`x\text{ = }\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`
`\begin{gathered} \text{where a = }16,\text{ b = -34, c = 16} \\ x\text{ = }\frac{-(-34)\pm\sqrt[]{(-34)^2-4(16)(16)}}{2(16)} \\ x\text{ = }\frac{34\pm\sqrt[]{1156-1024}}{32} \\ x\text{ = }\frac{34\pm\sqrt[]{132}}{32} \end{gathered}`
`\begin{gathered} x\text{ = }\frac{34\pm\sqrt[]{4*33}}{32} \\ x\text{ = }\frac{34\pm2\sqrt[]{33}}{32} \\ x\text{ = }\frac{2(17\pm\sqrt[]{33})\text{ }}{32}=\text{ }\frac{(17\pm\sqrt[]{33})\text{ }}{16} \\ x\text{ = }\frac{17+\sqrt[]{33}}{16}\text{ or }\frac{17-\sqrt[]{33}}{16} \\ x\text{ = 1.42 or }0.70 \end{gathered}`

The values of t to the nearest hundredth are 1.42 or 0.70