Question

Use the compound interest formula A(t)=P(1+ \frac{r}{n})^{nt} and round to the hundredths place, if necessary. Do not include commas in your answers.An account is opened with an initial deposit of$6500 and earns 3.6% interest compounded semi-annually. What will the account be worth in 20 years? AnswerHow much would the account have been worth if the interest were compounding weekly? Answer

Answer 1

We need to use the formula:

`A(t)=P(1+(r)/(n))^(nt)`

to find the worth of the account in 20 years.

We know that:

`\begin{gathered} P=6500 \\ r=3.6\%=0.036 \\ n=2 \\ t=20 \end{gathered}`

Thus, we obtain:

`\begin{gathered} A(20)=6500\cdot(1+(0.036)/(2))^(2\cdot20) \\ \\ A(20)=6500\cdot(1+0.018)^(40) \\ \\ A(20)=6500\cdot(1.018)^(40) \\ \\ A(20)=13268.58 \end{gathered}`

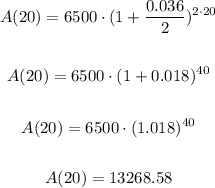
Therefore, the account, after 20 years, will be worth $13268.58.

If the interest were compounded weekly, n would be:

`n=(365)/(7)\cong52`

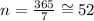
Then, the account would have been worth:

`\begin{gathered} A(20)=6500\cdot(1+(0.036)/(52))^(52\cdot20) \\ \\ A(20)=6500\cdot(1+(0.036)/(52))^(1040) \\ \\ A(20)\cong13350.49 \end{gathered}`

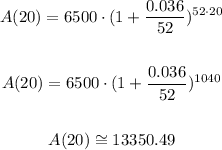
Notice that if we do not approximate the number of weeks (n) to 52, and instead use its exact value (365/7), then we obtain:

`A(20)=6500\cdot\mleft(1+(0.036)/((365)/(7))\mright)^{(365)/(7)\cdot20}\cong13350.50`

If the interest were compounded weekly, the account would have been worth $13350.49 (using n = 52).