Answer:
the equation is satisfied by the expression for z
Explanation:
Given z = y/(y² -a²x²) you want to show that it satisfies a second-order partial derivative equation.
Partial derivatives

and ...
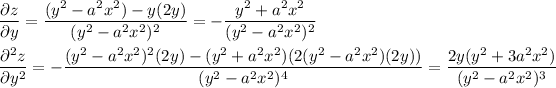
We can define ...
q = 2y(y²+3a²x²)/(y²-a²x²)³
so the equation of (b) becomes ...
(a²q) - a²(q) = 0 . . . . . . true
The given expression for z satisfies the partial differential equation.
__
Additional comment
We used the power rule and the quotient rule for derivatives. Tedious, but not difficult.