Question

Select the correct answer. Which exponential equation is equivalent to this logarithmic equation? log 7 ⁡ 6 + 3 ⁢ log 7 ⁡ 2 = x A. x 7 = 12 B. 7 x = 12 C. 7 x = 48 D.

Answer 1

The exponential equation that is equivalent to the given logarithmic equation is:

• 
  `\boxed{7^x=48}`

Explanation:

Use log rules to find the exponential equation that is equivalent to the given logarithmic equation.

Given logarithmic equation:

`\log_76+3\log_72 = x`

`\textsf{Apply the log power law:} \quad \log_ax^n=n\log_ax`

`\implies \log_76+\log_72^3 = x`

Simplify 2³ = 8:

`\implies \log_76+\log_78 = x`

`\textsf{Apply the log product law:} \quad \log_axy=\log_ax + \log_ay`

`\implies \log_7(6 \cdot 8)= x`

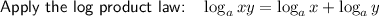
Multiply the numbers in the parentheses:

`\implies \log_748= x`

`\textsf{Apply log law:} \quad \log_ab=c \iff a^c=b`

`\implies 7^x=48`