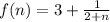ANSWER
Step-by-step explanation
Let's analyze this sequence. All given terms have the same whole part, 3, and the denominator of the fractional part starts at 3 the denominator of each is equal to the previous denominator plus 1.
So, for n = 1, which is the first term, the fractional part's denominator is 3, which is 2 more than 1. For n = 2, the second term, the denominator is 2 more than 2, and so on.
Since the whole part is constant, 3, we can conclude that the formula for each term, f(n) is: