Question

Find the tangent of each acute angle in the triangle below. Select all that apply.

Answer 1

Note that in any right triangle, the tangent of an acute angle is the opposite side divided by the adjacent side.

From the problem, we have a missing side that can be obtain using the Pythagorean Theorem.

`c^2=a^2+b^2`

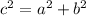
where c is the hypotenuse, a and b are the legs of the triangle.

So we have, c = 17 and a = 8

`\begin{gathered} 17^2=8^2+b^2 \\ 289=64+b^2 \\ 289-64=b^2 \\ 225=b^2 \\ b=\sqrt[]{225} \\ b=15 \end{gathered}`

Now we have the side 15.

In a right triangle, there are two accute angles.

The lower left and the upper right.

For the lower left angle, the opposite side is 8 and the adjacent side is 15.

So the tangent of this angle is 8/15

For the upper right angle, the opposite side is 15 and the adjacent side is 8.

So the tangent of this angle is 15/8

ANSWER :

8/15 and 15/8