Solution:
Given the function:
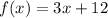
To find the inverse,
step 1: Let y represent f(x).
Thus,
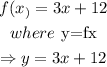
step 2: Swap the position of y for x.
Thus,
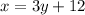
step 3: Make y the subject of the equation in step 2.
Thus,
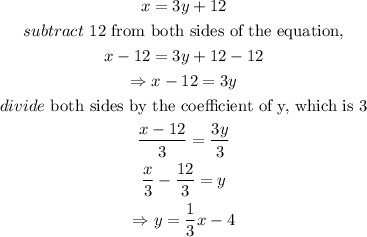
Thus, the inverse of the function is
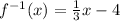
The graphs of the function and its inverse are as shown below: