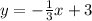Question

What is the equation of a line, in slope-intercept form, that is parallel to y=(-1/3)x + 5 and a y-intercept of ( 0, 3 ).

Answer 1

`y=-(1)/(3)x+3`

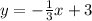
Step-by-step explanation:

Given:

`\begin{gathered} y=-(1)/(3)x+5 \\ And\text{ }y-intercept\text{ of }(0,3) \end{gathered}`

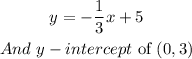
To find:

The equation of a line, in slope-intercept form, that is parallel to the above line

Recall that the slope-intercept form of the equation of a line is given as;

`y=mx+b`

where;

m = slope of the line

b = y-intercept of the line

Comparing the given equation with the slope-intercept equation, we can see that the slope(m) is -1/3 and y-intercept(b) is 5.

Note that parallel lines have the same slope. So a line that is parallel to the given line will have the same slope of -1/3.

Given the y-intercept of the parallel line as 3, we can go ahead and write the equation of the parallel line as seen below;

`y=-(1)/(3)x+3`