The original point is: (4, 1)
First transformation:
After the first transformation (4,1) becomes (1,4).
This transformation is a reflection across the line y=x. Because the rule for a reflection across the line y=x is:

Since after the transformation the point (4,1) became (1,4), we can see that the x coordinate was interchanged with the y coordinate.
Thus, the transformation that occurred here was a reflection across the line y=x.
Second transformation:
The previous point was (1,4) and with this second transformation, it became the point (1,-4). The x coordinate is the same, but the y coordinate changed its sign to a negative sign. The transformation that occurred here is: Reflection across the x-axis.
Because the rule for a reflection across the x-axis is:
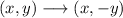
The x coordinate stays the same, and the y coordinate changes its sign.
Thus, the transformation was: a reflection across the x-axis.
Third transformation:
The previous point was (1,-4) and after the third transformation, the point is (-1,4). As you can see both the x-coordinate and the y-coordinate changed sign. The transformation is: a rotation of 180° about the origin.
Because the rule for this rotation is:

Both coordinates change of sign.
Thus, the transformation in this part was: rotation of 180° about the origin.
Answer:
reflection across the line y=x.
reflection across the x-axis.
rotation of 180° about the origin.