Question

Hi, can you help me with this question, please, thank you:)

Answer 1

Since the 5 hits can be any of the 7 attempts, we first need to calculate a combination of 7 choose 5.

The formula for a combination of n choose p is:

`C(n,p)=(n!)/(p!(n-p)!)`

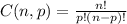
So we have:

`C(7,5)=(7!)/(5!(7-5)!)=(7\cdot6\cdot5!)/(5!\cdot2!)=(7\cdot6)/(2)=21`

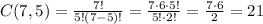
Now, if the probability of hitting is 0.28, the probability of missing is 1 - 0.28 = 0.72

Then, for the final probability, we can use the formula:

`\begin{gathered} P=C(7,5)\cdot(0.28)^5\cdot(0.72)^2 \\ P=21\cdot(0.28)^5\cdot(0.72)^2 \\ P=0.0187 \end{gathered}`

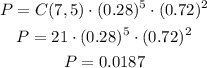
So the probability is 0.0187.