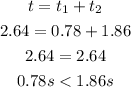Question

A popular entertainment at some carnivals is the blanket toss. see photo. (a) If a person is thrown to a maximum height of 28.0 ft above the blanket how long does she spend in the air ( b) Is the amount of time the person is above a height of 14.0ft more than, less than or equal to the amount of time the person is below a height of 14.0ft? Explain (c) Verify your answer to part b with calculation.

Answer 1

a. 2.64 seconds

b. The amount of time the person is above a height of 14 ft more than to the amount of time the person is below a height of 14 ft

c. 0.78 s < 1.87 s

Explanation:

a.

We can calculate the time using the following formula:

`\begin{gathered} h=u\cdot t+_{}(1)/(2)g\cdot t^2 \\ h=\text{ height }=\text{ 28 ft} \\ u=0\text{ m/s} \\ g=32.2\text{ }(ft)/(s^2) \end{gathered}`

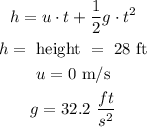
Replacing and solving for t:

`\begin{gathered} 28=0\cdot t+(1)/(2)\cdot32.2\cdot t^2 \\ t^2=28\cdot(2)/(32.2) \\ t=\sqrt[]{1.74} \\ t=1.32\text{ s} \end{gathered}`

Time would be double, as it rises and as it falls:

`\begin{gathered} t=2\cdot1.32 \\ t=2.64\text{ s} \end{gathered}`

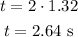
Therefore, the time spent in the air is 2.64 seconds

b.

More than, this is because as you goes up, your speed decreases, and as a result, the time you take to the top is longer.

Therefore: "The amount of time the person is above a height of 14 ft more than to the amount of time the person is below a height of 14 ft"

c.

We must calculate the initial velocity and the velocity at the midway, to be able to justify the above.

We calculate the initial velocity like this:

`\begin{gathered} v=\sqrt[]{2gh} \\ v=\sqrt[]{2\cdot32.2\cdot28} \\ v=42.46\text{ ft/s} \end{gathered}`

We calculate the midway velocity as follows:

`\begin{gathered} V=\sqrt[]{v^2-gh} \\ \text{replacing} \\ V=\sqrt[]{42.46^2-32.2\cdot28} \\ V=30.02\text{ m/s} \end{gathered}`

Thus, the time taken by her to reach the midway from the initial point is:

`\begin{gathered} t_1=(42.46-30.02)/(32.2) \\ t_1=0.39\text{ s} \end{gathered}`

While the return time would be:

`t_{1\text{lower}}=2\cdot t_1=2\cdot0.39=0.78`

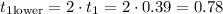
Now, the time it takes from the midway point to the highest point would be (the speed at the highest point is 0)

`\begin{gathered} t_2=(30.02-0)/(32.2) \\ t_2=0.93 \end{gathered}`

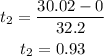
While the return time would be:

`t_{2\text{lower}}=2\cdot t_2=2\cdot0.93=1.86\text{ s}`

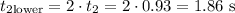
Therefore:

`\begin{gathered} t=t_1+t_2 \\ 2.64=0.78+1.86 \\ 2.64=2.64 \\ 0.78s<1.86s \end{gathered}`