Question

For positive acute angles A and B, it is known that tan A = 3/4 and cos B = 12/37.Find the value of cos(A + B) in simplest form.

Answer 1

cos (A + B) = - 57 / 185

Explanation:

First we draw the triangle containing angle A

From the above, we find that the length of the hypotenuse is 5; therefore,

`\begin{gathered} \sin A=(3)/(5) \\ \cos A=(4)/(5) \end{gathered}`

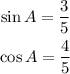
Now we draw the triangle containing angle B.

The length of the vertical side from Pythagoras's theorem is 35; therefore,

`\sin B=(35)/(37)`

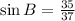
Now,

`\cos A+B=\cos A\cos B-\sin A\sin B`

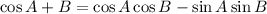
Putting in the values of cos A, cos B, sin A, and sin B we found above gives

`\cos A+B=((4)/(5))((12)/(37))-((3)/(5))((35)/(37))`
`\boxed{\cos A+B=-(57)/(185)}`

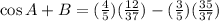
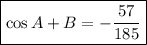
which is our answer!