Answer:
the magnitude F of the total friction force is 2456.7 lb
Step-by-step explanation:
Given the data in the question;
maximum speed = 35 mi/hr = ( 35×5280 / 60×60) = 51.3333 ft/s
diameter = 200ft
radius = 200/2 = 100 ft
First we calculate the normal component of the acceleration;
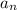 = v² / p
= v² / p
where v is the velocity of the car( 51.3333 ft/s)
p is the radius of the curvature( 100 ft)
so we substitute
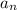 = (51.3333 ft/s)² / 100ft
= (51.3333 ft/s)² / 100ft
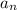 = (2635.1076 ft²/s²) / 100ft
= (2635.1076 ft²/s²) / 100ft
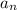 = 26.35 ft/s²
= 26.35 ft/s²
we convert Feet Per Second Squared (ft/s²) to Standard Gravity (g)
1 ft/s² = 0.0310809502 g
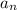 = 26.35 ft/s² × 0.0310809502 g
= 26.35 ft/s² × 0.0310809502 g
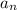 = 0.8189g
= 0.8189g
Now consider the dynamic equilibrium of forces in the Normal Direction;
∑
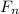 = m
= m
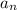
F = m
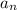
we know that mass of the car is 3000-lb = 3000lb(
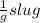 /1 lb)
/1 lb)
so
we substitute
F = 3000lb(
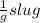 /1 lb) × 0.8189g
/1 lb) × 0.8189g
F = 2456.7 lb
Therefore; the magnitude F of the total friction force is 2456.7 lb