Solution
since the center is at the origin,
The equation of a circle is given as;

Since its passing through the point (5, -3)
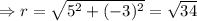
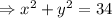
differentiating both sides with respect to x

At point (5, -3)
The slope m = dy/dx at (5, -3)
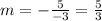
Hence the equation of tangent is given as;

Hence, the equation of tangent is y = 5/3x -34/3