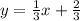To determine the equation of a line we can use the point-slope form:

Where
m is the slope of the line
(x₁,y₁) are the coordinates of one point on the line.
Since we know two points that are crossed by the line (5,6) and (-1,3) we can calculate the slope of the line using the following formula:
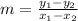
Where
(x₁,y₁) are the coordinates of one point of the line
(x₂,y₂) are the coordinates of a second point of the line
Replace the formula using
(x₁,y₁) = (5,6)
(x₂,y₂) = (-1,3)
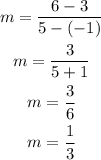
The slope of the line we are looking for is m=1/3
Next is to replace the coordinates of one of the points, for example (5,6) and the slope m=1/3 in the point-slope form to determine the equation of the line:
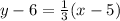
If you need to express the equation in the slope-intercept form you can dos as follows:
-First, distribute the multiplication on the parentheses term:
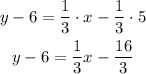
-Second, pass "-6" to the other side of the equation by applying the opposite operation, "+6" to both sides of it:
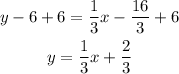
So the equation of the line that passes through points (-1,3) and (5,6) is