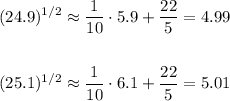Question

Find the local linear approximation of the function f(x)=(19+X) ^1/2 at x0=6, and use it to approximate (24.9)^1/2 and (25.1)^1/2

Answer 1

ANSWERS

• Linear approximation: ,y = (1/10)x + (22/5)

• (24.9)^1/2 ≈ 4.99

,

• (25.1)^1/2 ≈ 5.01

Step-by-step explanation

To find the local linear approximation of the function, we have to find the equation of the tangent line of the function at x = 6.

The equation of a line with slope m and y-intercept b is,

`y=mx+b`

The slope of a function at a particular point is the derivative of the function evaluated in that point.

Let's find the derivative of f(x) using the exponent rule,

`f^(\prime)(x)=(1)/(2)\cdot(19+x)^((1/2)-1)=(1)/(2(19+x)^(1/2))`

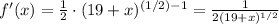
Now, evaluate at x = 6,

`f^(\prime)(6)=(1)/(2(19+6)^(1/2))=(1)/(2(25)^(1/2))=\frac{1}{2\sqrt[]{25}}=(1)/(2\cdot5)=(1)/(10)`

For now, the equation of the line is,

`y=(1)/(10)x+b`

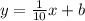
The function and the tangent line have the same value at the tangent point,

`f(6)=(19+6)^(1/2)=(25)^(1/2)=\sqrt[]{25}=5`

This means that the tangent point is (6, 5). We use this point to find the y-intercept of the tangent line,

`5=(1)/(10)\cdot6+b`

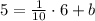
Solving for b,

`b=5-(6)/(10)=(22)/(5)`

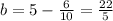
The linear approximation of f(x) is,

`y=(1)/(10)x+(22)/(5)`

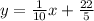
Now we want to use this to approximate (24.9)^1/2 and (25.1)^1/2. We have to use the values of x that, replacing in the function, would give the bases of these exponents:

`\begin{gathered} 24.9=19+x\Rightarrow x=24.9-19=5.9 \\ \\ 25.1=19+x\Rightarrow x=25.1-19=6.1 \end{gathered}`

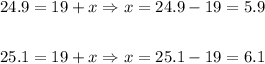
To find each approximation, we have to replace x with each of these values in the linear approximation of f(x). The approximate values are:

`\begin{gathered} (24.9)^(1/2)\approx(1)/(10)\cdot5.9+(22)/(5)=4.99 \\ \\ (25.1)^(1/2)\approx(1)/(10)\cdot6.1+(22)/(5)=5.01 \end{gathered}`