Given:
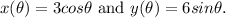
Required:
We have to draw the graphs of the given function.
Step-by-step explanation:
To draw the graph of the given functions proceeds as follows:
We know how to draw the graphs of sine and cosine functions. The given functions are multiples of sine and cosine.
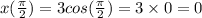
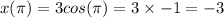
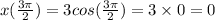
Hence the graph of the function is
Similarly,

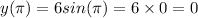
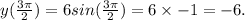
Hence the graph of the function is
Final answer:
Hence the final answer is the two graph above. That is
And