You have a system of 3 equations with 3 unknown variables.
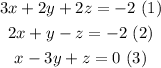
You can start by applying the reduction or elimination method to solve the system. Let's add equation (3) and equation (2)
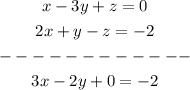
This will be equation (4).
Now, let's apply the same method to equation (1) and (2) but, first you need to multiply equation (2) by 2:
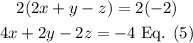
Add equation (1) and (5)
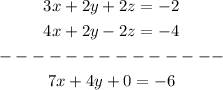
This will be equation (6).
Now, let's apply the elimination method again to equations (4) and (6). But, first let's multiply equation (4) by 2:
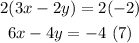
Now, let's add equations (6) and (7):
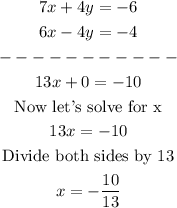
Now, you can replace this x-value into equation (6)

You know that x=-10/13, y=-2/13, now you can replace these values in any equation to find z-value:
Let's do it with equation (3)
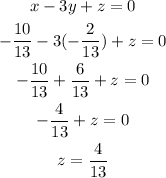
The answer is X=-10/13, Y=-2/13 and Z=4/13