Answer:
"I can find the maximum or minimum by looking at the factored expression of a quadratic function by reading off its roots and taking the arithmetic average of them to obtain the
 -coordinate of the quadratic function, and then substituting that value into the function."
-coordinate of the quadratic function, and then substituting that value into the function."
Explanation:
Because of the symmetry of quadratics (which is the case here because we have two factors of degree 1, so we are dealing with a polynomial of degree 2, which is a fancy way of saying that something is a quadratic), the
 -coordinate of the extremum (a fancy way of saying maximum or minimum) is the (arithmetic) average of the two roots.
-coordinate of the extremum (a fancy way of saying maximum or minimum) is the (arithmetic) average of the two roots.
In the factored form of a quadratic function, we can immediately read the roots: 3 and 7. Another way to see that is to solve
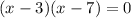 , which gives
, which gives
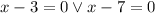 (the 'V' stands for 'or'). We can take the average of the two roots to get the
(the 'V' stands for 'or'). We can take the average of the two roots to get the
 -coordinate of the minimum point of the graph (which, in this case, is
-coordinate of the minimum point of the graph (which, in this case, is
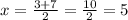 ).
).
Having the
 -coordinate of the extremum, we can substitute this value into the function to obtain the maximum or minimum point of the graph, because that will give the
-coordinate of the extremum, we can substitute this value into the function to obtain the maximum or minimum point of the graph, because that will give the
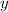 -coordinate of the extremum.
-coordinate of the extremum.