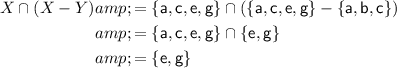Question

Solve for problem 25

Answer 1

`X \cap (X-Y)=\sf \{e,g\}`

Explanation:

Given sets:

• Universal, U = {a, b, c, d, e, f, g}
• X = {a, c, e, g}
• Y = {a, b, c}
• Z = {b, c, d, e, f}

Set Notation

`\begin{array} \cline{1-3} \sf Symbol & \sf N\:\!ame & \sf Meaning \\\cline{1-3} \{ \: \} & \sf Set & \sf A\:collection\:of\:elements\\\cline{1-3} \cup & \sf Union & \sf A \cup B=elements\:in\:A\:or\:B\:(or\:both)}\\\cline{1-3} \cap & \sf Intersection & \sf A \cap B=elements\: in \:both\: A \:and \:B} \\\cline{1-3} \sf ' \:or\: ^c & \sf Complement & \sf A'=elements\: not\: in\: A \\\cline{1-3} \sf - & \sf Difference & \sf A-B=elements \:in \:A \:but\: not\: in \:B}\\\cline{1-3} \end{array}`

(X - Y) is the difference between set X and set Y.

This means elements in set X but not in set Y.

X ∩ (X - Y) is the intersection of set X and set (X - Y).

This means elements that are in both sets.

Therefore:

`\begin{aligned}X \cap (X-Y)&=\sf \{a, c, e, g\}\cap\left(\{a, c, e, g\}-\{a, b, c\}\right)\\&=\sf \{a, c, e, g\}\cap\{e, g\}\\&=\sf \{e,g\}\end{aligned}`