Question

Which statements about the line that passes through (-2, 0) and (2, -4) are true?A. The slope of the line is 1. B. The line intersects the y-axis at (0, -2). C. The equation of the line is y = -x - 2D. The line intersects the x-axis at (-2, 0).

Answer 1

We are given the two points (-2, 0) and (2, -4)

We want to check the option(s) that is(are) correct as also given

Solution

Before we start considering the option, Let us find the slope and the equation of the line

The formula for finding slope (m) is given as

`m=(y_2-y_1)/(x_2-x_1)`

From the two points given

`\begin{gathered} x_1=-2 \\ y_1=0 \\ x_2=2 \\ y_2=-4 \end{gathered}`

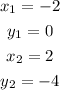
The slope (m) is

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(-4-0)/(2-(-2)) \\ m=(-4)/(2+2) \\ m=(-4)/(4) \\ m=-1 \end{gathered}`

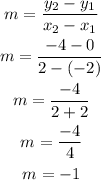
Obviously, Option A is False

Let us find the equation of the line

The formula to use is

`y-y_1=m(x-x_1)`

We now input the parameters

`\begin{gathered} y-y_1=m(x-x_1)_{} \\ y-0=-1(x-(-2)) \\ y=-(x+2) \\ y=-x-2 \end{gathered}`

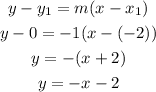
From here, One can see that Option B is True

Let us check for Option B now

To find the y-intercept

We put x = 0 in the equation we derived

From

`\begin{gathered} y=-x-2 \\ \text{put x = 0} \\ y=-0-2 \\ y=-2 \end{gathered}`

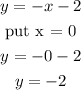
y-intercept is (0, -2)

Therefore, Option B is correct

We are left with option D

Indeed, (-2, 0) is part of the points given already

One can easily conclude that the line intersect the x-axis at (-2, 0)

Hence, Option D is True

The correct Option are B, C and D