Question

A principal of $4200 is invested at 6.75% interest, compounded annually. How many years will it take to accumulate $8000 or more in the account? (Use thecalculator provided if necessary.)Write the smallest possible whole number answer.

Answer 1

The annually compounded interest formula is:

`A=P(1+(r)/(n))^(n\cdot t)`

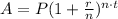
Where A is the amount you will have, P is the principal, r is the annual interest rate expressed as a decimal, n is the number of times the interest is compounded per time period (in this case as it is compounded annually, n=1) and t is the amount of time (in years) that the money is saved.

Then, we know that:

A=$8000

P=$4200

r=6.75%/100%=0.0675

n=1

t=?

Replace the known values and then solve for t as follows:

`\begin{gathered} 8000=4200(1+0.0675)^t \\ 8000=4200(1.0675)^t \\ (8000)/(4200)=(4200(1.0675))/(4200)^t \\ 1.9048=1.0675^t \\ Apply\text{ log to both sides} \\ \log 1.9048=\log 1.0675^t \\ By\text{ the properties of logarithms we have} \\ \log 1.9048=t\cdot\log 1.0675^{} \\ t=(\log 1.9048)/(\log 1.0675) \\ t=9.8647\approx10 \end{gathered}`

Therefore, it will take 10 years to accumulate $8000 or more in the account.