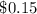Question

The answers are correct. How do you solve the equation, however, which leads to the right answers?"Kyd and North are playing a game. Kyd selects one card from a standard 52-card deck. If Kyd selects a face card (Jack, Queen, or King), North pays him $6. If Kyd selects any other type of card, he pays North $2.a) What is Kyd's expected value for this game? Round your answer to the nearest cent. -$0.15b) What is North's expected value for this game? Round your answer to the nearest cent. $0.15"

Answer 1

The probability of selecting face card (jack,queen or king) is

`\begin{gathered} P(\text{jack,queen or king)=}(4+4+4)/(52)=(12)/(52)=\: 0.23076 \\ \therefore P(\text{jack,queen or king)}=0.23076 \end{gathered}`

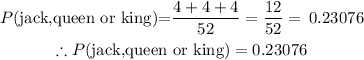
The probability of not selecting a face card (jack,queen or king):

`\begin{gathered} 1-0.23076=0.76924 \\ \therefore P(\text{not selecting face card)=}0.76924 \end{gathered}`

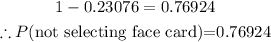
Therefore,

a) Kyd's Expected value is

`\begin{gathered} 0.23076*6-0.76924*2=1.38456-1.53848=-0.15392\approx-0.15(nearest\text{ cent)} \\ \end{gathered}`

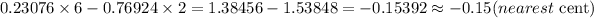
Hence, Kyd's Expected value is

`\text{ -\$0.15}`

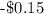
b) North's expected value is

`\begin{gathered} 0.76924*2-0.23076*6=0.15392\approx0.15(nearest\text{ cent)} \\ \end{gathered}`

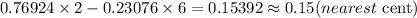
Hence, North's Expected value is

`\text{ \$0.15}`